This week or early next week, we’ll have the RavenDB 4.0 beta out. I’m really excited about this release, because it finalize a lot of our work for the past two years. In the alpha version, we were able to show off some major performance improvements and a few hints of the things that we had planned, but it was still at the infrastructure stage. Now we are talking about unveiling almost all of our new functionality and design.
The most obvious change you’ll see is that we made a fundamental change in how we are handle clustering. In prior versions of RavenDB, clusters were created by connecting together database instances running on independent nodes. In RavenDB 4.0, each node is always a member of a cluster, and databases are distributed among those nodes. That sounds like a small distinction, but it completely reversed how we approach distributed work.
Let us consider three nodes that form a RavenDB cluster in RavenDB 3.x. Each database in RavenDB 3.x is an independent entity. You can setup replication between different databases and out of the cooperation of the different nodes and some client side help, we get robust high availability and failover. However, there is a lot of work that you need to do on all the nodes (setup master/master between all the nodes on each can grow very tedious). And while you get high availability for reads and writes, you don’t get that for other tasks in the database.
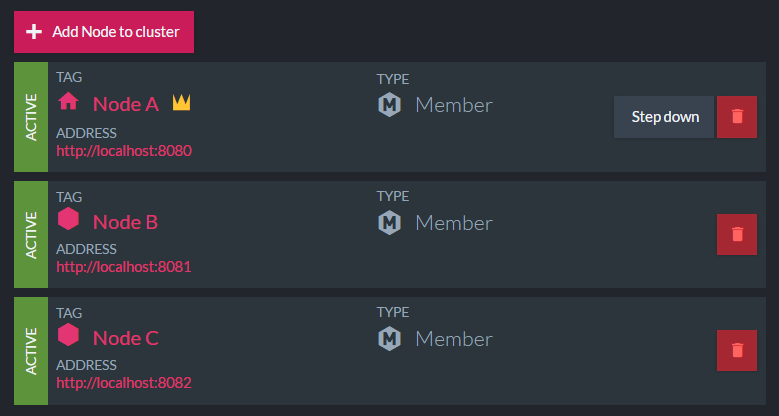
Let us see how this works in RavenDB 4.0, shall we? The first thing we need to do is to spin up 3 nodes.
As you can see, we have three nodes, and Node A has been selected as the leader. To simplify things to ourselves, we just assign arbitrary letters to the nodes. That allow us to refer to them as Node A, Node B, etc. Instead of something like WIN-MC2B0FG64GR. We also expose this information directly in the browser.
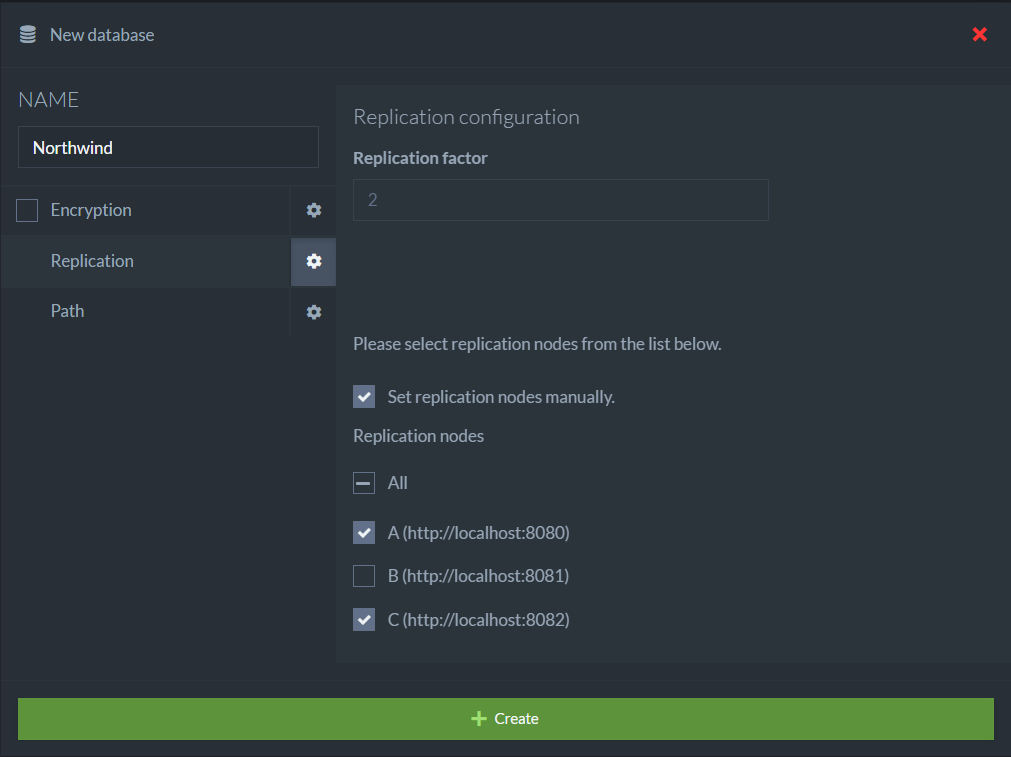
Once the cluster has been created, we can create a database, and when we do that, we can either specify what the replication factor should be, or manually control what nodes this database will be on.
Creating this database will create it on both A and C, but it will do a bit more than that. Those aren’t independent databases that hooked together. This is actually the same database, running on two different nodes. I created the sample data on Node C, and this is what I see when I look on Node A.
We can see that the data (indexes and documents) has been replicated. Now, let us see how we can work with this database:
You might notice that this looks almost exactly like you would use RavenDB 3.x. And you are correct, but there are some important differences. Instead of specifying a single server url, you can now specify several. And the actual url we provided doesn’t make any sense at all. We are pointing it to Node B, running on port 8081. However, that node doesn’t have the Northwind database. That is another important change. We can now go to any node in the cluster and ask for the topology of any database, and we’ll get the current database topology to use.
That make it much simpler to work in a clustered environment. You can bring in additional nodes without having to update any configuration, and mix and match the topology of databases in the cluster freely.
Another aspect of this behavior is the notion of database tasks. Here are a few of them.
Those are tasks (looks like we need to update the icon for backup) that are defined at the database level, and they are spread over all the nodes in the database automatically. So if we defined an ETL task and a scheduled backup, we’ll typically see one node handling the backups and another handling the ETL. If there is a failure, the cluster will notice that and redistribute the work transparently.
We can also extend the database to additional nodes, and the cluster will setup the database on the new node, transfer all the data to it (by assigning a node to replicate all the data to the new node), wait until all the data and indexing is done and only then bring it up as a full fledged member of the database, available for failover and for handling all the routine tasks.
The idea is that you don’t work with each node independently, but the cluster as a whole. You can then define a database on the cluster, and the rest is managed for you. The topology, the tasks, failover and client integration, the works.