Graph DB Sharding Strategies: Gravity
This is pure “scratch an itch” design post, since I started thinking about the topic, I might as well put my thoughts in a structured format. I am going to use twitter for this example, and assume that my end goal is to be able to do graph traversal, not just finding neighbors. Applying this to other social network scenarios should be pretty easy.
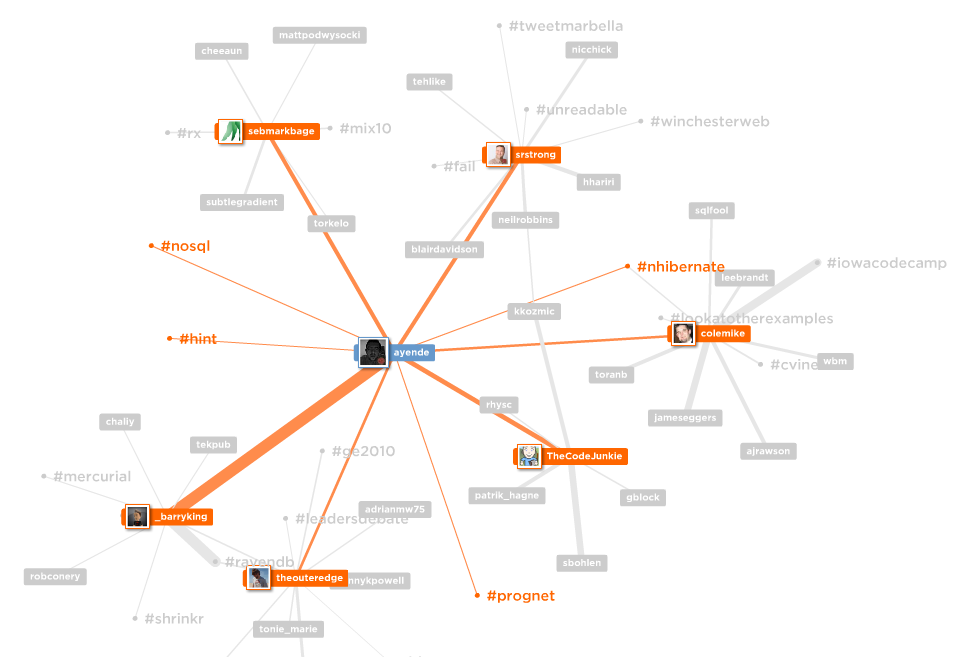
I generated this graph using this tool, this works using mentions, rather than following / followers graph, though. It will server to give you an idea what I am talking about.
One of the fundamentals of computer science is: localizing data leads to greater read performance. This is true whatever we are talking about keeping the data in the CPU L1 cache or in a distributed networked system. Typically, part of a sharding strategy is to keep all the data related to a root in a single location. The problem is, of course, that graphs don’t really have roots. And in most social network graphs, there is no such thing as a closed graph. There are, on average, ~7 million users within three hops from any twitter user. Now, it would be very easy to put 7 millions users to a single machine, except, as they say, they aren’t the same 7 million users.
Given that, I think that I can come up with an approach to allow more efficient queries and higher localization in the graph. The model assume an open and dynamic model (indeed, it relies on that).
We starts with geographical distribution. When we create a new user, we will place it in a shard dedicate to the geographical location the user is located on. This is a piece of data that we can get cheaply, and it has the advantage that users that interact with their circle of physical friends would tend to be clustered together anyway.
Next, we start assigning weights to associations. We only take into account outgoing associations (which solve the problem with outliers for incoming associations such as @aplsuk), but with a small twist, the weight of each outgoing association is taken as a portion of the total number of outgoing associations. In other words, the value of an outgoing association when you are following 10 friends is 0.1, but when you are following 500 friends, the value of each association is 0.002.
Next, we place some value on each mention that the user twits. A mention indicate that the association is active. For that matter, we probably need to create silent associations if a user keep mentioning someone that they are not following. For now, we will say that this value is 1% of the value of an association. That means that if I am following 100 users and I mentioned another user a hundred time, the value of the association is 0.02.
How does gravity comes into play here? Well, each outgoing association exact a pull on a node. But moving a node between shards is expensive, so we give shards an escape velocity. When we check if we need to re-shard a node, we aggregate the pulls of all the associations per node. Only if one shard pull is higher than the current shard pull + escape velocity will the node be shifted to the new shard.
Over time, this will tend to migrate most users close to the users that they are actively associated with. With that in mind, we can now move of to queries.
As I mentioned, I am interested more in this for graph traversal, and the good thing about this approach is that for the most part, most of the relevant information is located on the same shard. When the times comes to perform a query, we can assert that queries, too, need to have an escape velocity to cross a shard boundary. Unless there are enough outgoing connections to a given shard to overcome the escape velocity, outgoing connections to that shard are ignored. We can limit the cost of remote calls further if we increase the escape velocity for the query as the query search deeper. In other words, the escape velocity at depth = 0 would be 10, at depth = 1 it would be 100, at depth = 2 it would be 1000, etc.
While this represent a loss in accuracy of the results, it also mean that for the most case, results will tend to be more relevant.
Is this important if I don’t care for graph traversal?
There is another issue to consider, quite aside from graph traversal. The gravity approach outlined will tend to higher localization, and most operations are local. Consider writing a status update to all the people interested in that, when you have good locality, the cost of such on operation grows down drastically, in fact, I would say, it is highly likely that many such operations could be completed completely locally.






Comments
I don't know if this is the correct optimization. For example, I'm not a real known developer but people like you, Rob Conery, Scott Hanselman are. To me it seems that these people will end up in the same shard but is that really what you would want? It would only be interesting if al their followers would have the exact same interests in all these people who are actively related which I seriously doubt.
Ramon,
Nope, not at all.
Take a look at the actual numbers:
Ayende's friends: 59, Intersection with Rob: 4, Intersection With Scott: 0
Rob's friends: 31, Intersection with Ayende: 4, Intersection With Scott: 0
Scott's friends: 100, Intersection with Ayende: 0, Intersection With Rob: 0
Total intersection 0
Well, maybe Scott was a bad example ;-) what I ment was your weighting seems off to me. Weighting on geographical data is interesting for real friends but I'm using twitter for following / reading tweets that are related to my developer interests. My data read pattern thus based on my relation to the people I follow. I think that that is the most frequent access pattern for most people at least for our profession. People like Phil Haacked also tweet personal stuff but that isn't the reason why they follow him. If you would be very actively related with your mom then that still doesn't weight much for all his followers. Mentions having a weight which result you and your mom ending up on the same shard would not at all benefit the followers which read data I/O wise would benefit from being all on the same shard. Still this could result in I/O bottlenecks so maybe it would even be better to only put the 'profile' data on the same shard because these accounts are weighted to be related but not the tweet data as that could result in better I/O is those are scaled out.
With having a less weighted value when you follow more people. I think that doesn´t matter at all in the end when all follow associations would have that same weight strategy.
Another issue is that this is more based on recent behavior as in maybe even today. Because you are actively related today (thus high escape velocity) does not mean it would benefit your followers in read round-trip times at all to relocated all that data as it can just as easily be that you don't even be in a 'conversation' in the future.
However, this would strategy would benefit the 'active' users though. So if that would be the primary objective (having the best read/write performance between activity related users) then this would be a very good solution but we all know that it twitter is not about conversations its about eavesdropping conversations. Well, maybe not that secretly then ;-) but IMHO its all about listening to what others are doing/saying to learn and understand and that every 5 minutes all day long :-)
Sorry for all those typos :-) (RFC: add some edit functionalty to your blog)
I love the term "Escape velocity" for this algorithm. Is this a constant? it seems as though you could calculate based on the average load of the clusters what the escape velocity should be- to balance the cost of moving a node versus the benefit of lowering your shard load when it is needed.
Very interesting post though.
What you've described is a means to adjust where objects are sharded. Where do you end up storing the relations?
Also, when retrieving an object, how do you determine what shard it is in? Sorry not to familiar with object databases. I'm thinking in terms of memcached where any server can determine the server an object is on just by looking at its identity key. Maybe you do not care about knowing what server the object is on, if it can still be located via a map/reduce operation going to all servers.
fschwiet,
Relations are stored along with the node.
This scheme requires a master list of node id to shard id.
If you already use gravity as analogy I am wondering whether other fundamental forces could also be useful, e.g. repulsive forces between nodes without any relations between them (compare to electromagnetism with equal polarity - maybe introducing a non-relation with negative weigth between unrelated nodes?) or higher escape velocities for strongly related nodes (compare to strong nuclear force). Indeed, modeling that last force correctly would support the breaking up of clusters that grow too big (compare to radioactivity).
No, I am not joking. Reality's force model is incredibly ingenious and I love relating it to other stuff...
There's another problem with this algorithm: when the accumulated node mass exceeds certain threshold everything will collapse under the gravity force and a black hole will be formed.
hi Ayende,
nice post again! some interesting ideas there
to evolve to the dynamic nature of twitter it would be interesting to not only "strengthen" active relationships but also introduce a mechanism that forces older relationships to "decay"
for example, nobody gives a flying duck about what was tweeted 6 months ago... that data is basically forgotten by the users of twitter. I'm sure twitter themselves use it to mine for interesting patterns, but we as users do not
to deal with this we could timestamp all relationships, and then your "gravity" algo could reduce (halve?) the weight of those relationships as soon they are over a certain age... relationships would have a "half life"
the algorithm could consider relationship based on some probability, which is dictated by their weight... this may reduce computational complexity in a semantically meaningful way
regarding the geo-locality assumption, I think this is a better method than random initialization, but as others have mentioned I think it could be greatly improved. twitter just isnt as "local" as something like facebook
some other points (that only someone with better mathematical kung fu than I could answer):
how do we ensure shards have equal sizes? it may be that "gravity" converges to uneven shard sizes
how do we ensure the algorithm doesn't get trapped in a local minima?
IF it does produce useful results, how long does it take to converge to this state?
many more ???... :)
Alex
alex has a point that your model doesnt really account for access frequency, it sort of presumes they're all accessed with similar frequency.
I wonder, since you are building the indexes used to access the objects, if you should keep some statistics in the indexes. Consider tracking for each object instance how many times its accessed from each shard. Overall number of accesses will tell you if this item is hot and worth moving. Weight per shard will tell you where it belongs.
There may be some 0.1% of objects whose access frequencies are high enough to justify replicating them across shards.
This kind of weighting wouldn't detect entire groups that could be moved together, but it would work well for fine tuning. Maybe some grouping detector could run and move larger clumps around.
Comment preview