A few months ago I asked this question, and since then I’ve been asking it from some candidates. This is my 2nd tier question, and answering this correctly is going to give you quite a few brownie points.

The idea is to implement this interface:

But the only field that you can put in the implementation is a 32 KB byte array. See the original post for the full details.

Let us get rid of the easy stuff first, since the only value I can keep is a 32 KB byte array, saving and loading the values is trivial:

We can just save and load it directly, nothing much to do except validate that the size match on load.

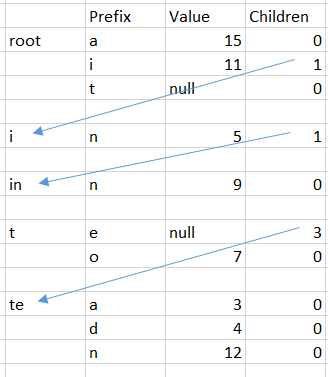
Now, let us see what we need to do, here is an example of a trie:

Typically, you would implement that using nested dictionaries, but that isn’t going to work given this exercise limitations.

So let us consider a more primitive alternative. We need to store the following information about each node in the trie. We start by defining the following node:

This wouldn’t work for the limits we have, but we are going to be building this in pieces. So this is an important step to understand how we go about it.

We are going to store the data in the following format:

So on each level, we are able to jump to the next stage and check its values. Searching for the right value in the children array is going to be simply a matter of doing  binary search on the children array.

The full code listing is linked from the bottom of the post, if you want to see it in context.

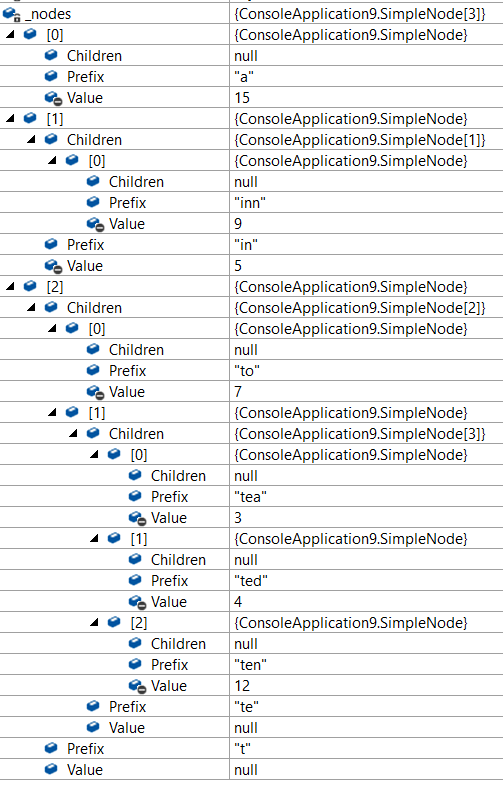
And here it is when it is stored as an object tree. Note that each child store the full key, not just the part it owns, because it make it easier to visualize.

Let us look at how we are building this kind of trie. We’ll start with two pretty simple helper methods.

There isn’t much to really see here, FindDifference will find the first difference between two strings from a given offset and FindMatch does a standard binary search on the array. The only special thing here is the fact that we are returning the match position even if we failed, we needed that to be able to know where to put the next entry. This will be clear when we’ll look at the Insert method.

This is quite a bit of code, but it can neatly divide into three separate options. In the first case, we reach an empty section in the tree, so we can just create a new leaf and call it a day. This is why we use a ref variable here, because it allows us to mutate the given parameter, which can be either the root, or the array on a nested node.

If there are already values at this level, we check if we need to go into the next level (creating the new level if necessary).

If there isn’t a value at this level that start with the current prefix, we just add it to this level as a value.

Pretty simple, once you break it down. The fun part about this is that as written, this is actually safe for multi threaded use, so a single write can make modifications at the same time that multiple readers can read, without any need for synchronization.

Reading from the trie given this structure is pretty simple:

We simply use the same logic as before, but because we have to make no changes, this is much simple to work with.

The last bit that we still need to handle is the deletes. Here is how this is handled.

That is basically the inverse of Insert, but it need to handle patching up the trie on the way back up again.

And this is pretty much it, right?

Except… that this is not what I started with. Where is the byte array? We are allocating memory here like crazy and all we did was implement a pretty standard trie without the use of dictionaries.

What is the point?

Well, now that we have this implementation, we have a good understanding on what is actually required of us, and we can take this code and move it to the array, but that would be in the next post.

In the meantime, you can read the entire code in one go here.