I mentioned earlier that B+Trees are a gnarly beast to implement properly. On the face of it, this is a really strange statement, because they are a pretty simple data structure. What is so complex about the implementation? You have a fixed size page, you add to it until it is full, then you split the page, and you are done. What’s the hassle?

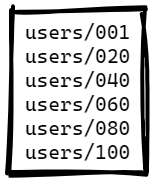
Here is a simple scenario for page splits, the following page is completely full. We cannot fit another entry there:

Now, if we try to add another item to the tree, we’ll need to split the page, and the result will be something like this (we add an entry with a key: users/050):

How did we split the page? The code for that  is really simple:

As you can see, since the data is sorted, we can simply take the last half of the entries from the source, copy them to the new page and call it a day. This is simple, effective, and will usually work just fine. The key word here is usually.

Given a B+Tree that uses variable size keys, with a page size of 4KB and a maximum size of 1 KB for the keys. On the face of it, this looks like a pretty good setup. If we split the page, we can be sure that we’ll have enough space to accommodate any valid key, right? Well, just as long as the data distribution makes sense. It often does not. Let’s talk about a concrete scenario, shall we? We store in the B+Tree a list of public keys.

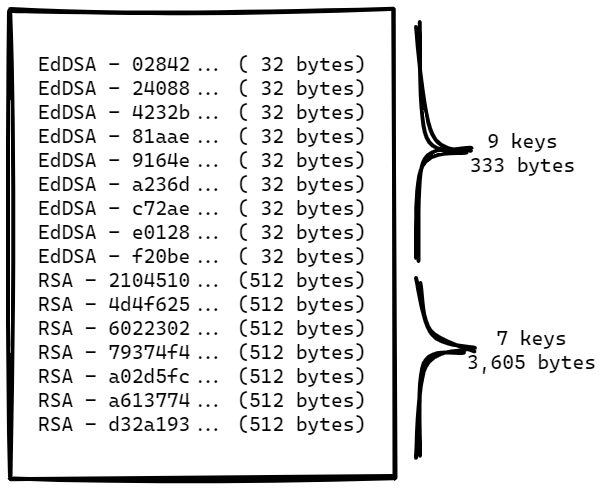
This looks like the image below, where we have a single page with 16 entries and 3,938 bytes in use, and 158 bytes that are free. Take a look at the data for a moment, and you’ll notice some interesting patterns.

The data is divided into two distinct types, EdDSA keys and RSA keys. Because they are prefixed with their type, all the EdDSA keys are first on the page, and the RSA keys are last. There is a big size difference between the two types of keys. And that turns out to be a real problem for us.

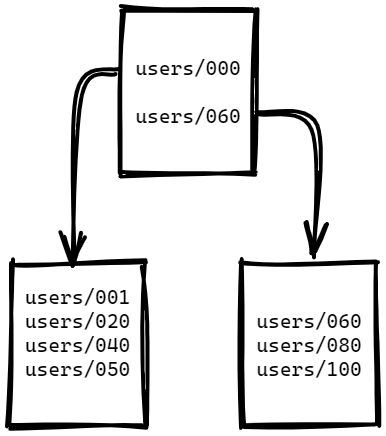
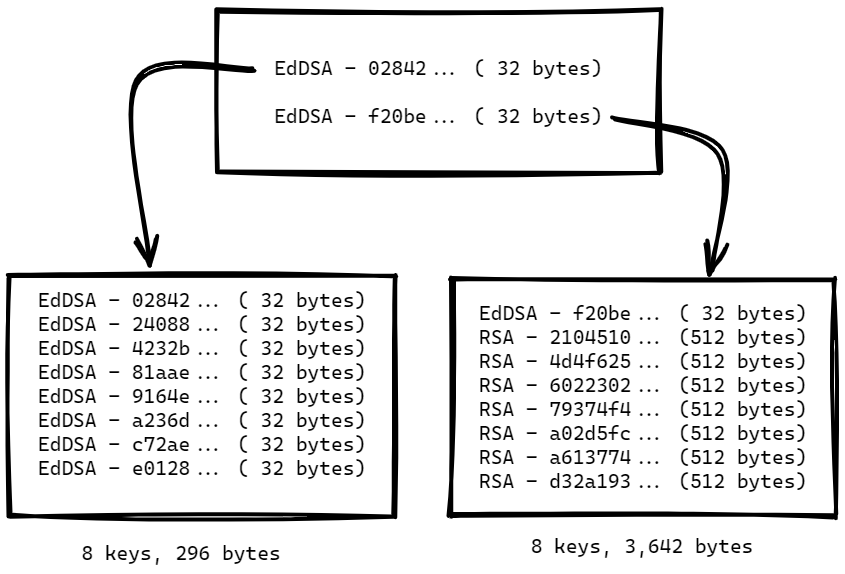
Consider what will happen when we want to insert a new key to this page. We still have room to a few more EdDSA keys, so that isn’t really that interesting, but what happens when we want to insert a new RSA key? There is not enough room here, so we split the page. Using the algorithm above, we get the following tree structure post split:

Remember, we need to add an RSA key, so we are now going to go to the bottom right page and try to add the value. But there is not enough room to add a bit more than 512 bytes to the page, is there?

What happens next depends on the exact implementation. It is possible that you’ll get an error, or another split, or the tree will attempt to proceed and do something completely bizarre.

The key here (pun intended) is that even though the situation looks relatively simple, a perfectly reasonable choice can hide a pretty subtle bug for a very long time. It is only when you hit the exact problematic circumstances that you’ll run into problems.

This has been a fairly simple problem, but there are many such edge cases that may be hiding in the weeds of B+Tree implementations. that is one of the reasons that working with production data is such a big issue. Real world data is messy, it has unpredictable patterns and stuff that you’ll likely never think of. It is also the best way I have found to smoke out those details.