Huffman coding and encoding compressed data
So far, we have dealt with relatively straightforward topics. Given a corpus, find a shared dictionary that we can then use to extract repeated patterns. This is the classic view of compression, even if real world compression schemes are actually a lot more convoluted. Now, that we have compressed text like the following, what comes next?
<-43,6>11,'n<-60,6>Anna Nepal<-40,13><-18,8><-68,8>awest@twinte.gov'}
Obviously, it would be pretty important to encoding this properly. Here is an example of a bad encoding scheme:
[prefix – byte – 1 for compressed, 0 for literal]
[length – int – length of compressed / literal]
[offset – int – back reference if the prefix was set to 1]
The problem here is that we need 6 bytes to encode a one letter literal, and 9 bytes to encode any back reference. Using this inefficient method, encoding the compressed string above actually takes more space than the original one.
As you can imagine, there has been a lot of research into this. The RFC 1951 specification, for example, set us how to do that in detail, although I find this explanation much easier to go through.
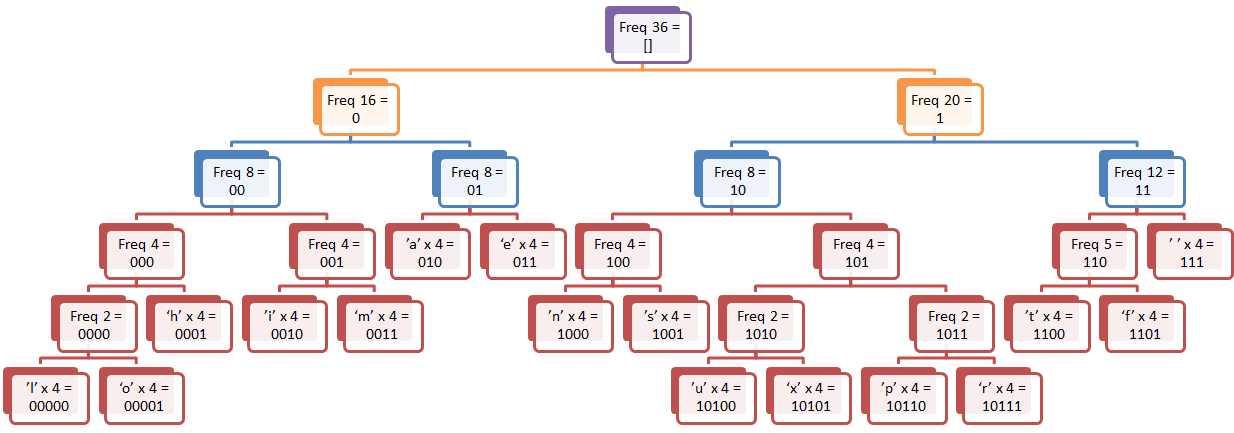
Let us see a simple Huffman encoding scheme. We will use “this is an example of a huffman tree” as our text, and first, we’ll build the table.
And now we can encoding the above sentence in 135 bits, instead of 288.
For decoding, we just run over the table again, and stop the first time that we hit a leaf.
For example, let us see how we would decode ‘ ‘ and ‘r’.
Space is very common, appearing 7 times in the text. As such, it is encoded as 111. So, start from the root, and move right three times. We are in a leaf node, and we output space.
With the letter R, it only appear in the text 4 times, and its encoding is 10111. So move right from the root node, then left, then three times right, resulting in the leaf node R.
So the results of Huffman encoding using the above table is:
[t] = 0001 [h] = 1010 [i] = 1011 [s] = 0000 [ ] = 111 [i] = 1011 [s] = 0000 [ ] = 111 [a] = 010 [n] = 0011 [ ] = 111 [e] = 011 [x] = 10001 [a] = 010 [m] = 0010 [p] = 10010 [l] = 110010 [e] = 011 [ ] = 111 [o] = 110011 [f] = 1101 [ ] = 111 [a] = 010 [ ] = 111 [h] = 1010 [u] = 10000 [f] = 1101 [f] = 1101 [m] = 0010 [a] = 010 [n] = 0011 [ ] = 111 [t] = 0001 [r] = 10011 [e] = 011 [e] = 011
However, we have a problem here, this result in 135 bits or 17 bytes (vs 36 bytes for the original code). However, 17 bytes contains 136 bits. How do we avoid corruption in this case? The answer is that we have to include an EOF Marker in there. We do that by just adding a new item to our Huffman table and recording this normally.
So, that is all set, and we are ready to go, right? Almost, we still need to decide how to actually encode the literals and compressed data. GZip (and FemtoZip) uses a really nice way of handling that.
The use of Huffman table means that it contains the frequencies of individual bytes values, but instead of having just 0 – 255 entries in the Huffman table, they uses 513 entries.
256 entries are for the actual byte entries.
256 entries are just lengths.
1 entry for EOF.
What does it means, length entries? It basically means, we store the values 256 – 511 for lengths. When we read the Huffman value, it will give us a value in the range of 0 – 512.
If it is 512, this is the EOF marker, and we are done.
If it is 0 – 255, it is a byte literal, and we can treat it as such.
But if it is in the range of 256 – 511, it means that this is a length. Note that because lengths also cluster around common values, it is very likely that we’ll be able to store most lengths in under a byte.
Following a length, we’ll store the actual offset back. And again, FemtoZip is using Huffman encoding to do that. This is actually being done by encoding the offset into multiple 4 bits entries. The idea is to gain as much as possible from commonalities in the actual byte patterns for the offset.
Yes, it is confusing, and it took me a while to figure it out. But it is also very sleek to see this in action.
On my next post, I’ll bring it all together and attempt to actually generate something that produces compressed data and can decompress it back successfully…






Comments
With huffman coding you need at least one bit to encode anything. With arithmetic coding you can encode symbols (and lengths) in less than a bit. Now that is even sleeker...
I think there are some errors in the list. For example, according to the table, 't' is 1100, but is 0001 in the list.
When dealing with text, you will still want to encode using Huffman Coding than Arithmetic Coding; because in text spaces you still have a skewed probabilistic distribution. Neither dictionaries like in this case, nor transformations like the Burrow-Wheelers would change the underlying redundancy of the data.
For example: In English/Spanish the probability of spaces and vowels is far higher than consonants.
For other data types like images you will probably want to use Arithmetic coding, however, after you apply blocking techniques like DCT/Wavelets you end up having to test if those distributions are best encoded using one or the other.
If I am remembering correctly from my pass on the data compression course. JPEG uses Huffman codes after a DCT/RLE
Federico, the only reason to choose Huffman over arithmetic is speed and simplicity. In terms of compression arithmetic coding is never worse than Huffman.
What I meant was that you still want to encode using Huffman because you are not winning much using Arithmetic Coding in text spaces and the speed tradeoff can make a difference (even if integer implementations of AC are quite good). Especially when dealing with big text based datasets like the ones that the typical user of RavenDB would handle.
For the general case, I agree with you Arithmetic Coding is the safe bet if what you are looking is compressed as much as you can.
@Federico: This makes no sense. With skewed distributions (as in text only input) arith coding can encode some frequent symbols (space, double quotes) in less than 1 bit or for instance in 1 bit and half. Saving half a bit on the most frequent symbols can amount to massive savings in total.
Comment preview